占星術のアスペクト「カイト」は、どんな意味や性格になる？

カイトは複合アスペクトです。

いくつかのアスペクトが組み合わさり「幾何学図形」を作っているのです。

ですので、普通のアスペクトよりも強力な力を発揮することになります。

本日は、占星術のアスペクト「カイト（Kite）」について

･･･などを考えてみます。

カイトの意味や性格

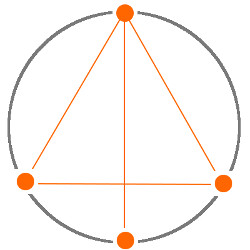
カイトは、どんな意味があるのでしょうか？

カイト（Kite）を日本語にすると、凧（タコ）ですね。

確かにこの図形は、糸で三角凧を上げているように見えます。

「幸運の三角形」を大空にあげることができるのですね♡

 幸運の力を外に向けて発揮できる

カイトは、グランドトリンがベースになっています。

それに加えて、180度の位置に惑星があります。

これは、グランドトリンという幸運の力を外に向けて発揮する形になります。

また、180度に位置した惑星は、隣の惑星と60度（セクスタイル）の関係になります。

60度は協力関係ですから、そこでも幸運の力をスムーズに発揮しやすくなるのです。

 他の元素の協力を得て、アグレッシブになる

グランドトリンは、ある意味「自己完結的」でした。

風なら風、火なら火と、同じ元素の三角形となります。ですので、安定はしていています。

でも、他の元素の協力がないので、外に働きかける力が弱いのです。

しかし、カイトは他の元素の協力を得ることができるので、アグレッシブに動くことができます。

松村先生は「何となくふわふわした恵まれたグランドトリンの資質は消え、生き方にドライブ感が出てくる」とおっしゃってます。

 大きなテーマを見つけ、社会に打ちだすと良い

カイトは、グランドトリンという幸運パワーを外に向けて発揮できます。

この複合アスペクトを持っている人は、自分の才能を社会に向けて打ち出してゆくことを心がけた方がよさそうです。

松村先生は

･･･との旨をおっしゃってます。

カイトを持っている有名人

では、ホロスコープにカイトを持っている有名人は誰でしょうか？

 ドリス・デイ

カイトを持っている有名人には、女優・歌手のドリス・デイがいます。

「センチメンタル・ジャーニー」や「ケセラセラ」を大ヒットさせた人ですね。

夢のある熱いパワーを、世界に広げて行く

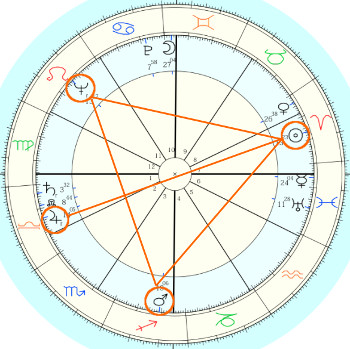
ドリス・デイは

･･･です。

夢のある熱いパワーを、世界に広げて行く･･･そんな感じがする配置ですね。

実際、ドリス・デイの明るい人柄やドリーミーな歌声に、世界中が魅了されました。

私もその一人です（笑）

夢をあきらめず、世界に働きかけ続けたドリス・デイ

ドリス・デイは、幼い頃から歌や踊りが大好きで、バレリーナを目指していました。

ですが、15歳の時に列車事故にあい、バレエを断念します。

また、2度の離婚後、再婚した夫との死別などを経験しています。

そんな困難はありましたが、夢をあきらめませんでした。

歌の練習に専念し、レス・ブラウン楽団の専属歌手となります。

そして「センチメンタル・ジャーニー」をヒットさせ、後に「ケセラセラ」を大ヒットさせます。

また、女優としても「二人でお茶を」「カラミティージェーン」などで世界的人気を得るのです。

 新庄剛志さん

カイトを持つ有名人は、新庄剛志さんもいます。

若干ゆるいアスペクトですが、

…のカイトになっています。

グランドトリンの力を海王星が外に打ち出している

新庄さんの理解不能な行動。

これは、グランドトリンの力を海王星が外に向かって打ち出しているのでしょう。

海王星ですから、とてもミステリアス。そして「夢のある形」で広がってゆきます。

まとめ

本日は、占星術のアスペクト「カイト」の意味や性格、有名人の例について解説しました。

まとめると、

･･･です。

ホロスコープ鑑定する際、このアスペクトがあったら、「なにか大きなことを実現できそうな人」と思って良いかもしれませんね。

今回の記事は「完全マスター西洋占星術」を参考にしています。